
To construct a specific finite volume method of the form ( 19) one needs to specify suitable approximations to F i + 1 2 (the numerical flux) and S i (the numerical source) in integrals ( 20). Relation ( 19) is exact, even if it looks like a finite difference approximation. (20) Q i n = 1 Δ x ∫ x i − 1 2 x i + 1 2 Q ( x, t n ) d x, F i + 1 2 = 1 Δ t ∫ t n t n + 1 F Q x i + 1 2, t d t, S i = 1 Δ t Δ x ∫ t n t n + 1 ∫ x i − 1 2 x i + 1 2 S ( Q ( x, t ) ) d x d t. They showed that under certain conditions, a large monomolecular system could be modeled well by a lower-order system. The results obtained by Wei and Prater gave rise to a question: “How do we lump components into suitable pseudocomponents with proper accuracy?” Wei and Kuo determined conditions for exact ( Wei and Kuo, 1969) and approximate ( Kuo and Wei, 1969) lumping for monomolecular and pseudo-monomolecular reaction systems. Wei and Prater also established a specially designed experiment for identifying these pseudocomponents. 1 〈 l, c〉 is the concentration of a pseudocomponent. If lK = λ l, then d l c / d t = l c λ, where the standard inner product. These linear combinations or “pseudocomponents” correspond to the left eigenvectors (row vectors) l of a kinetic matrix K as follows. They showed that for systems in which only monomolecular or pseudo-monomolecular reactions occur, a linear combination exists of concentrations that change in time independently. In their classical paper, Wei and Prater (1962) introduced a so-called lumping procedure. Marin, in Advanced Data Analysis & Modelling in Chemical Engineering, 2017 4.3.8 Lumping Analysis Hence, for a given matrix E, the disturbance de-coupling problem can be solved iff a matrix H can be found which requires the following rank condition:ĭenis Constales. In this situation, the residuals also have low sensitivity to uncertainties due to approximate de-coupling. On the other hand, if the required eigenstructure is not perfectly assignable, the eigenvectors must be chosen to be close in a least-squares sense, to the desired eigenvectors. If the desired observer eigenstructure is assignable (using the left or right eigenvectors), perfect de-coupling can be achieved. If QCE = 0 and all columns of the matrix E are right eigenvectors of Ac corresponding to any eigenvalues, Eq. If the left eigenvector assignability condition is not satisfied, a suitable choice of right eigenvectors can be assigned as columns of the matrix E.
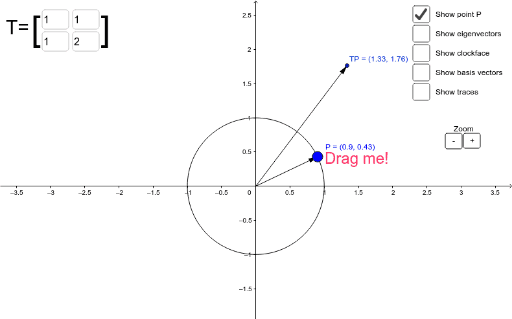
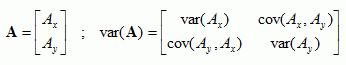
We will use the two statements “T > 0 and r i ∈ N, i = 1, 2,…, m, are proper” and “the sampling rates are proper” interchangeably.Īssume that T > 0 and r i ∈ N, i = 1, 2,…, m, are proper.


 0 kommentar(er)
0 kommentar(er)
